栈学习
约 1670 字大约 6 分钟
数据结构
2025-03-04
本文作者:程序员飞云
栈的特征
栈和其他线性表最大的区别是,插入和删除只能在一端进行操作,满足顺序:后进先出
插入元素的操作称为入栈(Push)
删除元素的操作称为出栈(Pop)
例如我们现在模拟元素[1,2,3]出栈和入栈操作
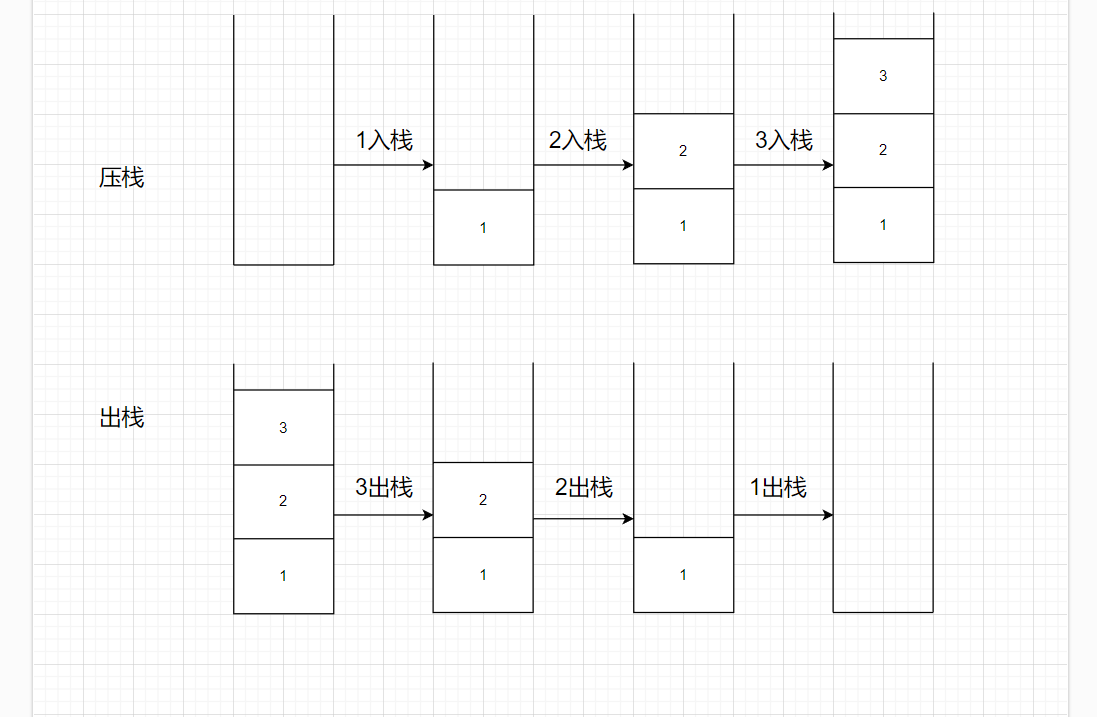
栈的出栈顺序
入栈顺序为 1,2,3,4,元素可能的出栈顺序是什么?
这个题目就和栈的特性有关,题目只说了入栈,但是没说出栈的顺序。
可能的出栈顺序如下:总共14种情况,其余情况都是不可能的。
4,3,2,1: 最简单的就是依次入栈,然后逆序出栈
1,2,3,4: 元素每次入栈后就立即出栈
1,2,4,3: 1入栈出栈,2入栈出栈,3入栈,4入栈出栈,3出栈
1,3,2,4: 1入栈出栈,2入栈,3入栈出栈,2出栈,4入栈出栈
1,3,4,2: 1入栈出栈,2入栈,3入栈出栈,4入栈出栈,2出栈
1,4,3,2: 1入栈出栈,2入栈,3入栈,4入栈出栈,3出栈,2出栈
2,1,3,4: 1入栈,2入栈出栈,1出栈,3入栈出栈,4入栈出栈
2,1,4,3: 1入栈,2入栈出栈,1出栈,3入栈,4入栈出栈,3出栈
2,3,1,4: 1入栈,2入栈出栈,3入栈出栈,1出栈,4入栈出栈
2,3,4,1: 1入栈,2入栈出栈,3入栈出栈,4入栈出栈,1出栈
2,4,3,1: 1入栈,2入栈出栈,3入栈,4入栈,3出栈,2出栈,1出栈
3,2,1,4: 1入栈,2入栈,3入栈出栈,2出栈,1出栈,4入栈出栈
3,2,4,1: 1入栈,2入栈,3入栈出栈,2出栈,4入栈出栈,1出栈
3,4,2,1: 1入栈,2入栈,3入栈出栈,4入栈,2出栈,1出栈
栈的操作
push: 元素入栈pop: 元素出栈peek: 栈顶元素empty: 栈是否为空
数组实现栈
此处采用top指向栈顶元素,元素在top-1处
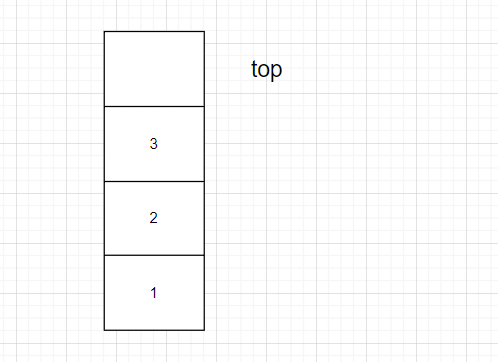
数组会存在扩容的问题,所以针对数组我们还需要再写一个扩容机制。
1. 定义数组stack,元素位置top,初始化配置
/**
* 存放栈元素
*/
private Object[] stack;
/**
* 栈顶位置
*/
private int top;
/**
* 初始化数组长度
*/
public ArrayStack() {
stack = new Object[10];
}2. 元素入栈
因为是数组,所以我们需要手写一个扩容机制
/**
* 数组扩容
* @param size
*/
public void expandCapacity(int size) {
int len = stack.length;
if (size > len) {
size = size*3/2+1; // 每次扩大50%
stack = Arrays.copyOf(stack, size);
}
}/**
* 元素入栈
*
* @param value
*/
public void push(T value) {
expandCapacity(top+1);
stack[top] = value;
top++;
}3. 栈顶元素
/**
* 查看栈顶元素
*
* @return
*/
public T peek() {
T t = null;
if (top > 0) {
t = (T) stack[top - 1];
}
return t;
}4. 元素出栈
/**
* 元素出栈
*
* @return
*/
public T pop() {
T peek = peek();
if (top > 0) {
stack[top - 1] = null;
top--;
}
return peek;
}5. 栈内元素是否为空
/**
* 判断栈是否为空
*
* @return
*/
public boolean isEmpty() {
return top == 0;
}全部代码
public class ArrayStack<T> {
/**
* 存放栈元素
*/
private Object[] stack;
/**
* 栈顶位置
*/
private int top;
/**
* 初始化数组长度
*/
public ArrayStack() {
stack = new Object[10];
}
/**
* 元素入栈
*
* @param value
*/
public void push(T value) {
expandCapacity(top+1);
stack[top] = value;
top++;
}
/**
* 查看栈顶元素
*
* @return
*/
public T peek() {
T t = null;
if (top > 0) {
t = (T) stack[top - 1];
}
return t;
}
/**
* 元素出栈
*
* @return
*/
public T pop() {
T peek = peek();
if (top > 0) {
stack[top - 1] = null;
top--;
}
return peek;
}
/**
* 判断栈是否为空
*
* @return
*/
public boolean isEmpty() {
return top == 0;
}
/**
* 数组扩容
* @param size
*/
public void expandCapacity(int size) {
int len = stack.length;
if (size > len) {
size = size*3/2+1; // 每次扩大50%
stack = Arrays.copyOf(stack, size);
}
}
}链表实现栈
链表有点特殊,不是我们平常操作的尾插法插入到链表的后端,而是使用头插法,将链表逆序。
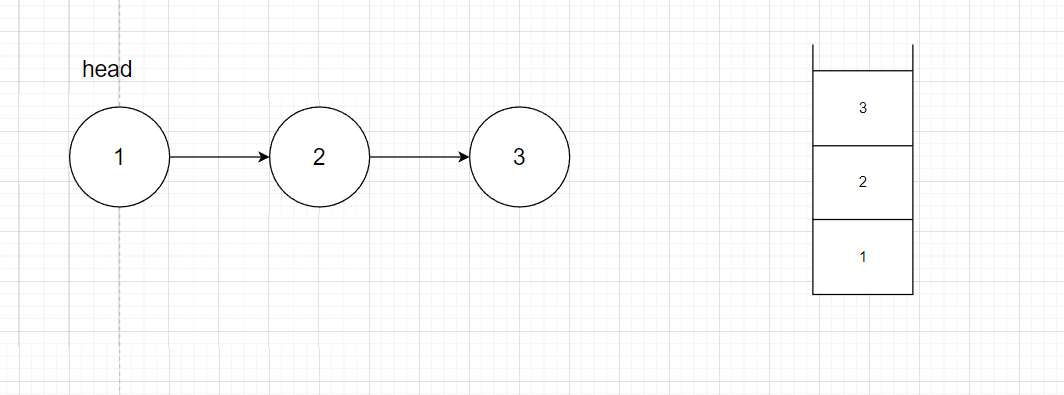
1. 定义链表节点
class Node<T> {
public T data; // 数据
public Node<T> next;
}2. 初始化链表
private Node<T> head; // 栈顶指针
public ListStack() {
head = null;
}3. 入栈
入栈需要考虑两种情况,第一种就是链表是空的,那么这个栈顶元素就是入栈的元素,第二种情况是链表不为空,那么此时需要记录当前的节点,然后创建新的节点头插法的方式插入到当前节点的前面。
/**
* 入栈操作
* @param data
*/
public void push(T data) {
if (head == null) {
head = new Node<T>();
head.data = data;
head.next = null;
} else {
Node<T> temp = head;
head = new Node<T>();
head.data = data;
head.next = temp;
}
}4. 栈顶元素
/**
* 获取栈顶元素操作
* @return
*/
public T peek() {
if (head == null) {
return null;
}
return head.data;
}5. 出栈
/**
* 出栈操作
* @return
*/
public T pop() {
if (head == null) {
return null;
}
T data = head.data;
head = head.next;
return data;
}6. 栈空
/**
* 判断栈是否为空
* @return
*/
public boolean isEmpty() {
return head == null;
}全部代码
public class ListStack<T> {
private Node<T> head; // 栈顶指针
public ListStack() {
head = null;
}
/**
* 入栈操作
* @param data
*/
public void push(T data) {
if (head == null) {
head = new Node<T>();
head.data = data;
head.next = null;
} else {
Node<T> temp = head;
head = new Node<T>();
head.data = data;
head.next = temp;
}
}
/**
* 栈顶元素操作
* @return
*/
public T peek() {
if (head == null) {
return null;
}
return head.data;
}
/**
* 出栈操作
* @return
*/
public T pop() {
if (head == null) {
return null;
}
T data = head.data;
head = head.next;
return data;
}
/**
* 判断栈是否为空
* @return
*/
public boolean isEmpty() {
return head == null;
}
}
class Node<T> {
public T data; // 数据
public Node<T> next;
}Java源码分析
Stack源码
public class Stack<E> extends Vector<E> {
public Stack() {
}
/**
* 元素入栈
*/
public E push(E item) {
addElement(item);
return item;
}
/**
* 元素出栈
*/
public synchronized E pop() {
E obj;
int len = size();
obj = peek();
removeElementAt(len - 1);
return obj;
}
/**
* 栈顶元素
*/
public synchronized E peek() {
int len = size();
if (len == 0)
throw new EmptyStackException();
return elementAt(len - 1);
}
public boolean empty() {
return size() == 0;
}
public synchronized int search(Object o) {
int i = lastIndexOf(o);
if (i >= 0) {
return size() - i;
}
return -1;
}
private static final long serialVersionUID = 1224463164541339165L;
}我们可以看到这个栈十分的简陋,基本上就是调用Vector里面的方法完成了入栈,出栈等操作,在里面还加上了synchronized来保证线程安全,但是一般不是太推荐使用这个,而是推荐使用ArrayDeque来进行操作,ArrayDeque提供了完整的操作。

以上我们操作的栈都是一端操作,即元素的出栈,入栈都是通过单端实现的,但是这个不大适用于一般的场景,一般使用ArrayDeque比较多
贡献者
flycodeu
版权所有
版权归属:flycodeu
