函数
约 2752 字大约 9 分钟
C++
2025-03-04
本文作者:程序员飞云
函数基本知识
函数的定义和调用
- 返回类型
- 函数名
- 参数
- 函数体
简单的平方函数
#include<iostream>
using namespace std;
int square(int x) {
int y = x * x;
return y;
}
int main() {
int res = square(2);
cout << res << endl;
}案例练习
- 求两个数的立方和
int cubeSum(int x, int y) {
return pow(x, 3) + pow(y, 3);
}- 求阶乘
int factorial(int n) {
int res = 1;
for (int i = 1; i <= n; i++) {
res *= i;
}
return res;
}- 复制字符串
将一个字符串复制n次,然后将结果返回
string copyStr(string str, int n) {
string res;
while (n > 0) {
res += str;
n--;
}
return res;
}局部变量的生命周期
局部变量只有在当前函数作用域里面可见
全局变量所有的作用域都可以访问
- 自动对象
程序执行到变量(形参)定义的语句时才开始创建,在程序运行完成后就销毁。
生命周期和作用域一样。
自动对象存放在栈里面。
- 静态对象
延长一个局部变量的生命周期,在作用域外面依然保留。
局部静态对象只有局部的作用域,在外块依然不可以访问,但是生命周期贯穿整个程序运行过程。
静态对象存放在静态存储区
int callCount() {
static int count = 0;
++count;
cout <<"调用次数" << count << endl;
return count;
}
int main() {
for (int i = 0; i < 5; i++)
{
callCount();
}
}
函数的声明
如果我们将函数放在main后面,就会找不到函数,所以我们需要使用函数声明来告诉编译器到什么地方执行这个函数。
直接在main上面写对应的定义函数,不需要方法体,还可以省略方法里面的参数名称
#include<iostream>
using namespace std;
// 函数声明
int cubeSum(int , int);
int factorial(int );
string copyStr(string , int );
int callCount() {
static int count = 0;
++count;
cout <<"调用次数" << count << endl;
return count;
}
int main() {
cout << cubeSum(2, 2) << endl;
cout << factorial(3) << endl;
cout << copyStr("hello", 3) << endl;
for (int i = 0; i < 5; i++)
{
callCount();
}
}
int cubeSum(int x, int y) {
return pow(x, 3) + pow(y, 3);
}
int factorial(int n) {
int res = 1;
for (int i = 1; i <= n; i++) {
res *= i;
}
return res;
}
string copyStr(string str, int n) {
string res;
while (n > 0) {
res += str;
n--;
}
return res;
}分离式编译和头文件
- 分离式编译
我们可以将不同的代码放在不同的文件里面,独立编译之后链接运行。
例如上面的复制字符串案例,我们只需要再另一个文件里面写好代码,然后通过函数的声明去找到这个函数
但是这样的缺点就是每次运行到对应的函数都需要使用一个函数声明,非常不便于管理。
- 头文件
我们可以将函数的声明放在头文件里,然后直接通过include来引入头文件,直接调用里面的方法。一般而言是将一些功能性的文件放入头文件中。
新建头文件utils.h
#pragma once
#include<string>
using namespace std;
int cubeSum(int x, int y) {
return pow(x, 3) + pow(y, 3);
}
int factorial(int n) {
int res = 1;
for (int i = 1; i <= n; i++) {
res *= i;
}
return res;
}
// 定义在其他的文件中
string copyStr(string, int);main引用
#include<iostream>
using namespace std;
#include "utils.h";
int callCount() {
static int count = 0;
++count;
cout <<"调用次数" << count << endl;
return count;
}
int main() {
cout << cubeSum(2, 2) << endl;
cout << factorial(3) << endl;
cout << copyStr("hello", 3) << endl;
for (int i = 0; i < 5; i++)
{
callCount();
}
}参数的默认值
// 错误,形参2必须要有默认值
void ca1(int num = 10, int num2) {
}
// 正确
void ca2(int num, int num2) {
}
// 正确
void ca3(int num = 10, int num2=10) {
}
// 正确
void ca4(int num , int num2=10) {
}参数要么都有默认值,要么都没有默认值,如果需要默认值,最后一个参数必须要有返回值。
函数的重载
函数名相同,参数不同(数量,类型)
参数传递
值传参数
值传递的问题,以下代码存在问题,n的值并不会改变,因为是直变量值复制,而不是针对原来的变量改变
#include<iostream>
using namespace std;
void increase(int x) {
++x;
}
int main() {
int n = 0;
increase(n);
cout << n << endl;
}可以使用指针,这样每次操作地址都会改变,也就能够实现参数修改。
void increase2(int* x) {
++(*x);
}
increase2(&n);引用形参
但是指针形参编写,还是有些麻烦的,我们可以直接使用引用,适用于这种不希望值拷贝的过程,如果在数据量大或者使用字符串的时候,就不适合采用这种直接值拷贝的方式,而是直接采用引用指向原地址。
// 引用形参
void increase3(int& x) {
++x;
}比如采用引用,就不需要进行值拷贝,效率较高
bool isLonger(string& str1, string& str2) {
return str1.size() > str2.size();
}使用常量做形参,避免对数据进行修改
bool isLonger(const string& str1, const string& str2) {
return str1.size() > str2.size();
}引用传参总结
- 传引用方便函数调用
- 传引用避免值拷贝
- 使用常量引用作为形参,避免数据更改
数组传递
最基础的数组传递
void printArray(const int arr []) {
}
void printArray2(const int * arr) {
}
void printArray3(const int arr [5]) {
}但是以上的数组都是采用的指针,本质上都是一样的,目前还无法获取数组长度。
- 数组长度作为形参
void printArray3(const int*arr,int size) {
}- 传入数组引用
void printArray4(const int (& arr)[5]) {
}可变形参
- (...):只能出现在形参列表的最后一个位置
- 初始化initializer_list:和vector类似,只能是常量值
- 可变参数模板
返回类型
无返回值
比如两个值互换,如果值相等就返回,必须要使用引用才能完成数据的交换,才能改变原始值
void swap(int& num1, int& num2) {
if (num1 == num2) {
return;
}
int temp = num1;
num1 = num2;
num2 = temp;
}
int main() {
int a = 10;
int b = 25;
swap(a, b);
cout << "a=" << a << endl;
cout << "b=" << b << endl;
}有返回值
函数调用点会创建一个临时量,用来保存函数调用的结果,当使用的return语句返回时,就会用返回值初始化这个临时量。
longstr(const string& str1, const string& str2) {
return str1.size() > str2.size() ? str1 : str2;
}但是如果我们不希望采用一个新的字符串来保存结果,我们可以将返回的字符串也变成引用,这样就不会创建一个新的内存空间来存储值
const string& longstr(const string& str1, const string& str2) {
return str1.size() > str2.size() ? str1 : str2;
}但是需要注意,如果返回的是一个局部变量的引用,比如

这是不安全的,因为局部变量使用完成后就销毁了,返回值是它的引用,而这个局部变量已经没了,也就无法进行引用这个变量。
返回数组指针


// 简化函数声明
typedef int arrayT[5];// 自定义的类型别名,长度为5
arrayT* fun2(int x);但是以上的返回还是有点繁琐,C++11提供了新的方式
尾置返回
auto fun3(int x) -> int(*)[5];递归
一个函数字节调用了自己方法。
递归三要素
- 递归的方法返回值,参数
- 终止条件
- 单层递归逻辑
#include<iostream>
using namespace std;
//递归方式求阶乘
int factorical(int num) {
if (num == 1) {
return num;
}
return num * factorical(num - 1);
}
int main() {
int add = factorical(3);
cout << "3!=" << add << endl;
}案例
斐波那契数列
1,1,2,3,5,8,13....
当前数字是前面两个数字的和
int fib(int n) {
if (n == 1 || n == 2) {
return 1;
}
return fib(n - 1) + fib(n - 2);
}案例
1. 二分查找
普通方法
/*
二分查找
arr 数组
n 数组长度
left左指针位置
right 右指针位置
target目标元素
*/
int searchBinary(const int (&arr)[], int n, int left, int right, int target) {
// 不存在
if (target<0 || target>n) {
return -1;
}
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (arr[mid] == target) {
return mid;
}
else if (arr[mid] > target) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
return -1;
}递归方法
这个里面采用到了引用,避免这个数组的值拷贝占据空间,而使用数组引用之后,可以在里面定义对应的长度大小
/*
二分查找递归法
arr 数组
n 数组长度
left左指针位置
right 右指针位置
target目标元素
*/
int searchBinary2(const int (&arr)[4], int left, int right, int target) {
// 不存在
if (target<arr[left] || target>arr[right] || left>right) {
return -1;
}
// 中间值
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid;
}
else if (arr[mid] > target) {
return searchBinary2(arr, left, mid - 1, target);
}
else {
return searchBinary2(arr,mid + 1, right, target);
}
}2. 快速排序
通过一次将整个数组元素通过一个元素分成两部分,左边部分元素值小于这个元素,右边元素值大于这个元素,然后再将左右两部分继续划分,直到最后划分完成
void quickSort(int(&arr)[5], int start, int end) {
if (start > end) {
return;
}
int left = start;
int right = end;
int mid = arr[(right + left) / 2];
while (left <= right) {
// 元素比中间值小,继续移动
while (left <= right && arr[left]<mid) {
left++;
}
// 元素比中间值大,继续移动
while (left <= right && arr[right] > mid) {
right--;
}
// left元素值大于mid,right元素值小于mid,交换元素
if (left <= right) {
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
left++;
right--;
}
}
// 递归左右部分
quickSort(arr, start, right);
quickSort(arr, left, end);
}3. 遍历二叉树
定义二叉树节点
struct TreeNode
{
int value;
TreeNode* left;
TreeNode* right;
};构建二叉树
// 1
// 2 3
// 4 6 7 5
TreeNode node7 = { 7,nullptr,nullptr };
TreeNode node6 = { 6,nullptr,nullptr };
TreeNode node5 = { 5,nullptr ,nullptr};
TreeNode node4 = { 4,nullptr,nullptr };
TreeNode node3 = { 3,&node7,&node5 };
TreeNode node2 = { 2,&node4,&node6 };
TreeNode root = { 1,&node2,&node3 };前序遍历
// 先序遍历 中左右
void preOrder(TreeNode* root) {
if (root == nullptr) {
return;
}
// 中
cout << root->value << "\t";
// 左
preOrder(root->left);
// 右
preOrder(root->right);
}
int main(){
// 1
// 2 3
// 4 6 7 5
TreeNode node7 = { 7,nullptr,nullptr };
TreeNode node6 = { 6,nullptr,nullptr };
TreeNode node5 = { 5,nullptr ,nullptr};
TreeNode node4 = { 4,nullptr,nullptr };
TreeNode node3 = { 3,&node7,&node5 };
TreeNode node2 = { 2,&node4,&node6 };
TreeNode root = { 1,&node2,&node3 };
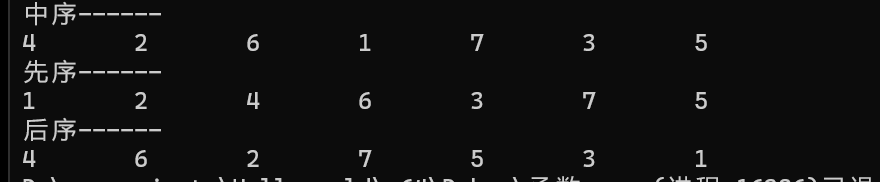
// 先序 1 2 4 6 3 7 5
preOrder(&root);
cout << endl;
}中序遍历
// 先序遍历 中左右
void preOrder(TreeNode* root) {
if (root == nullptr) {
return;
}
// 中
cout << root->value << "\t";
// 左
preOrder(root->left);
// 右
preOrder(root->right);
}
int main(){
// 1
// 2 3
// 4 6 7 5
TreeNode node7 = { 7,nullptr,nullptr };
TreeNode node6 = { 6,nullptr,nullptr };
TreeNode node5 = { 5,nullptr ,nullptr};
TreeNode node4 = { 4,nullptr,nullptr };
TreeNode node3 = { 3,&node7,&node5 };
TreeNode node2 = { 2,&node4,&node6 };
TreeNode root = { 1,&node2,&node3 };
// 中序 4 2 6 1 7 3 5
inOrder(&root);
cout << endl;
}后序遍历
// 后序遍历
void afterOrder(TreeNode* root) {
if (root == nullptr) {
return;
}
// 左
afterOrder(root->left);
// 右
afterOrder(root->right);
// 中
cout << root->value << "\t";
}
int main(){
// 1
// 2 3
// 4 6 7 5
TreeNode node7 = { 7,nullptr,nullptr };
TreeNode node6 = { 6,nullptr,nullptr };
TreeNode node5 = { 5,nullptr ,nullptr};
TreeNode node4 = { 4,nullptr,nullptr };
TreeNode node3 = { 3,&node7,&node5 };
TreeNode node2 = { 2,&node4,&node6 };
TreeNode root = { 1,&node2,&node3 };
// 后序 4 6 2 7 5 3 1
afterOrder(&root);
cout << endl;
}
贡献者
flycodeu
版权所有
版权归属:flycodeu
