树的学习
约 1786 字大约 6 分钟
数据结构
2025-03-04
树的概念
树是一个有n个有限节点组成的一个有层次关系的集合,每个节点有0个或者多个子节点,没有父节点的节点称为根节点。
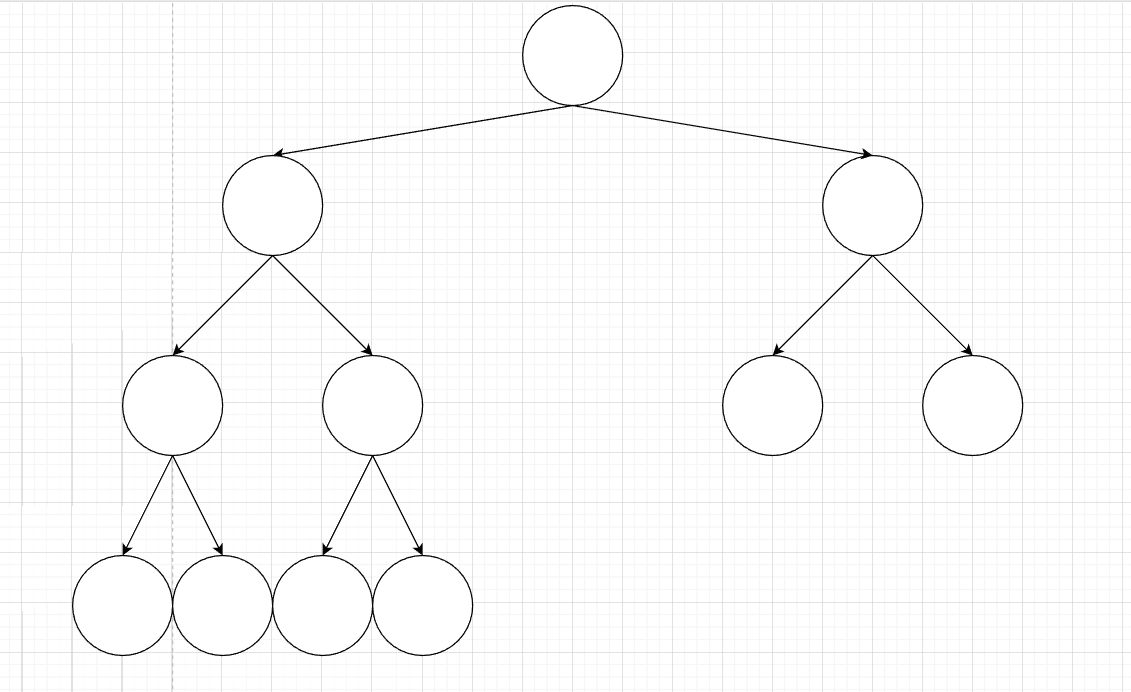
树还具有如下的相关概念:
- 节点的度:一个节点含有的子节点的个数
- 树的度:一棵树中最大节点的度称为树的度
- 叶子节点或终端节点:节点的度为0
- 非终端节点或分支节点:节点的不为0
- 双亲节点或父节点:一个节点含有子节点,那么这个节点就是子节点的父节点
- 孩子节点:一个节点含有子树的根节点
- 兄弟节点:具有相同的父节点的节点
- 节点的祖先:从根节点到该节点所经过分支上的所有节点
- 子孙:以某节点为根的子树中的任一节点
- 森林:由m(m>=0)棵互不相交的树的集合
- 无序树:树中任意节点的子节点之间没有任何顺序联系
- 有序树:树中任意节点的子节点之间由顺序关系
- 二叉树:每个节点最多含有两个子树的二叉树
树的性质
1. 二叉树的第i层的节点个数最多为2^(i-1)
意味着父节点的子节点一定只有左右两个节点,从2二层开始都能满足2^i的规律,但是第一层只有一个节点,所以节点最多为2^(i-1)
2. 深度为k的二叉树最多有2^k-1个节点
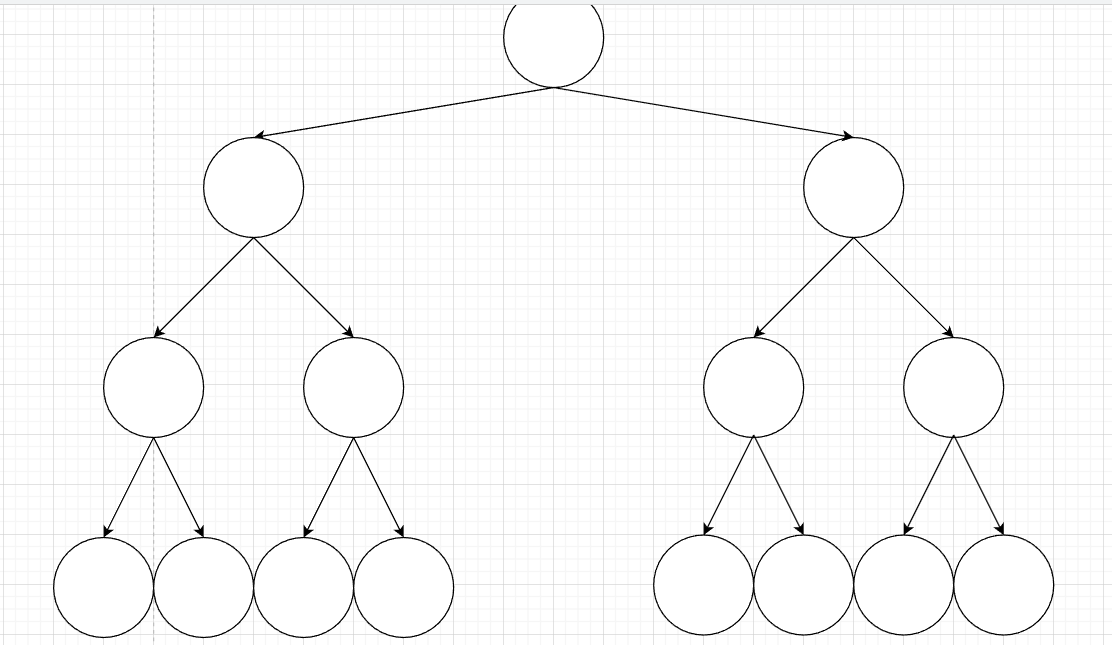
由于不同的教材对于深度和高度的有不同的理解,这里深度从1开始取,上面图的深度为4,所以总的节点个数最多为15个节点
3. 对于任意二叉树,叶子节点数为N0,而度为2的节点总数为N2,N0=N2+1
对于完全二叉树而言,总的节点数设置为N,有如下关系
N = N0+N1+N2
N = N0+2N2+1
4. 具有n个节点的完全二叉树的深度必为log2(n+1)
5. 对于完全二叉树,从上到下,从左到右,设置节点的编号为i,左孩子编号为2i,右孩子编号为2i+1,双亲编号为i/2
二叉树的分类
1. 满二叉树
只有度为0和度为2的节点,并且度为0的节点在同一层上
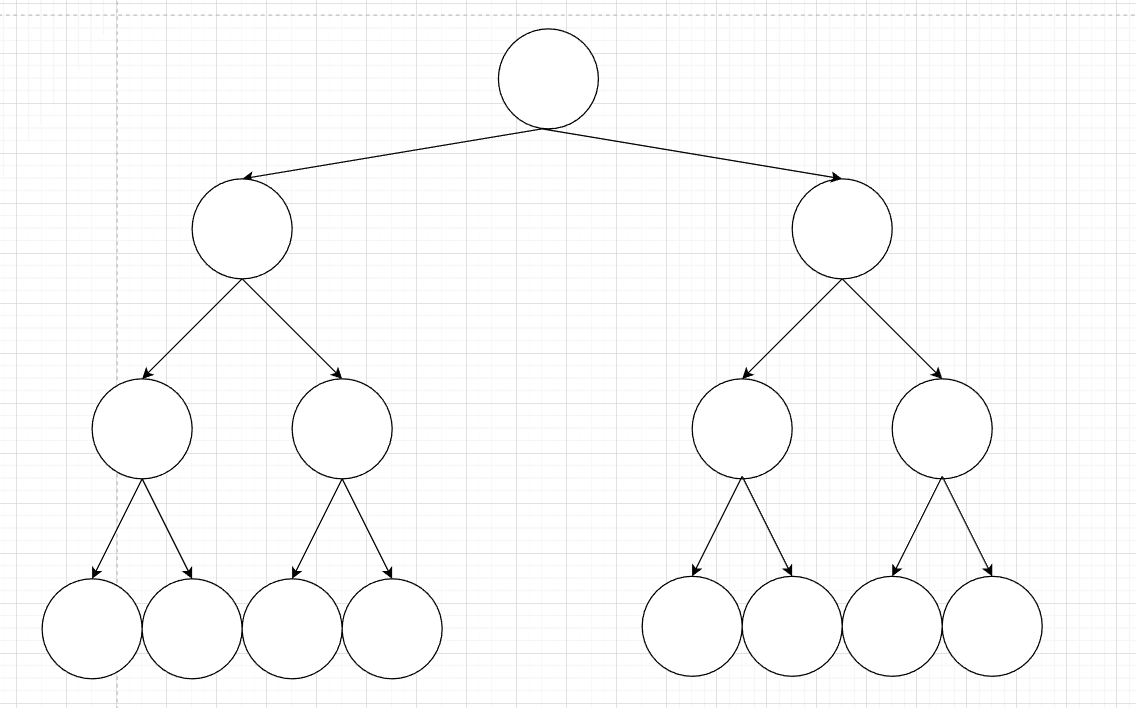
深度为k,有2^k-1个节点的二叉树
2. 完全二叉树
在完全二叉树中,除了最底层的节点没填满外,其余每层节点的树都达到最大的节点数,并且最下面一层节点都是集中在最左侧位置。若最底层为第 h 层(h从1开始),则该层包含 1~ 2^(h-1) 个节点。
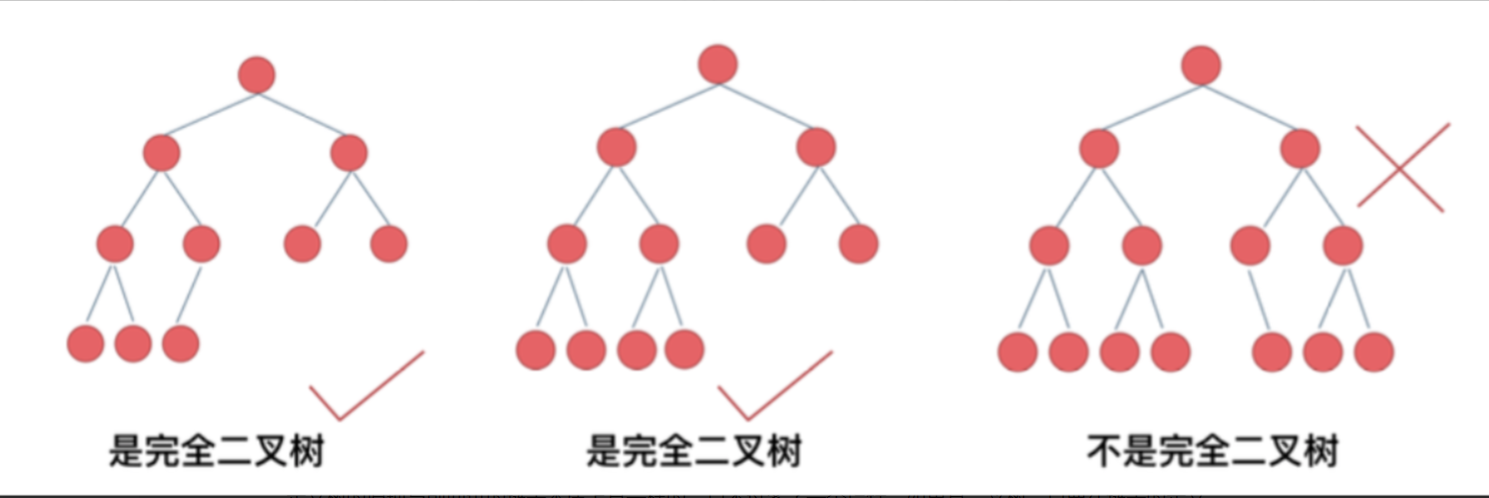
3. 二叉搜索树
- 左子树上所有的节点值都小于根节点的值
- 右子树上所有的节点值都大于根节点的值
- 他们的子树也同样适用这个规律
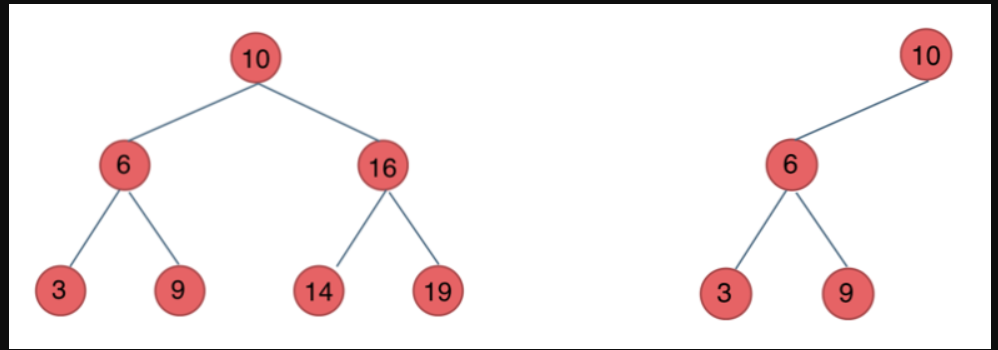
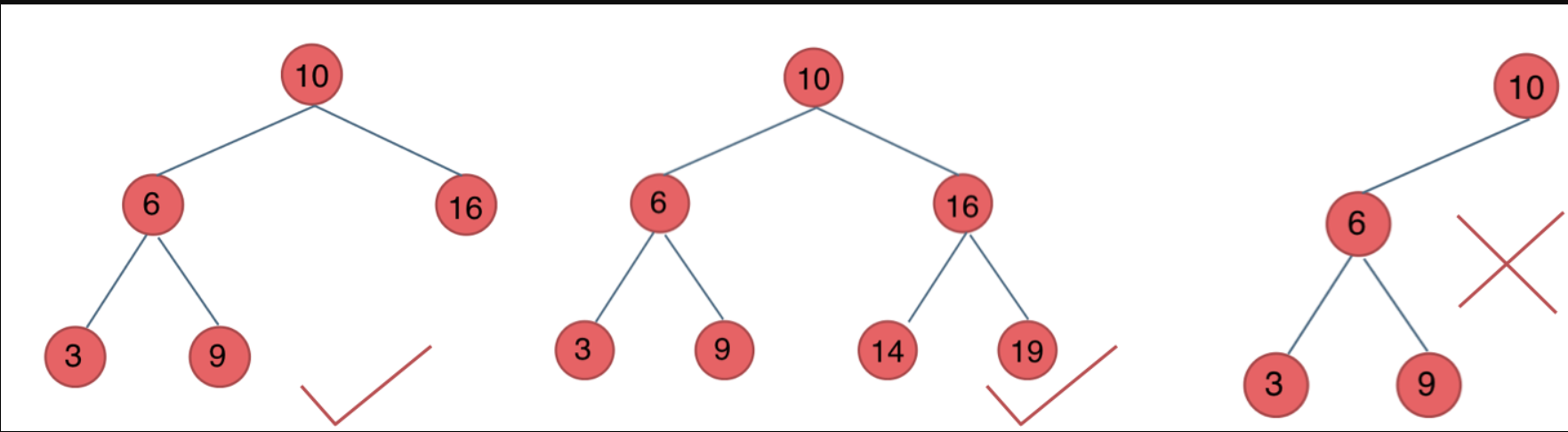
4. 平衡二叉搜索树
是一棵空树或者左右字数的高度不能相差超过1。
树的定义
二叉树的定义
public class TreeNode{
int data;
TreeNode leftChild;
TreeNode rightChild;
}N叉树的定义
public class TreeNode{
int data;
List<TreeNode> childern;
}树的存储方式
数组存储
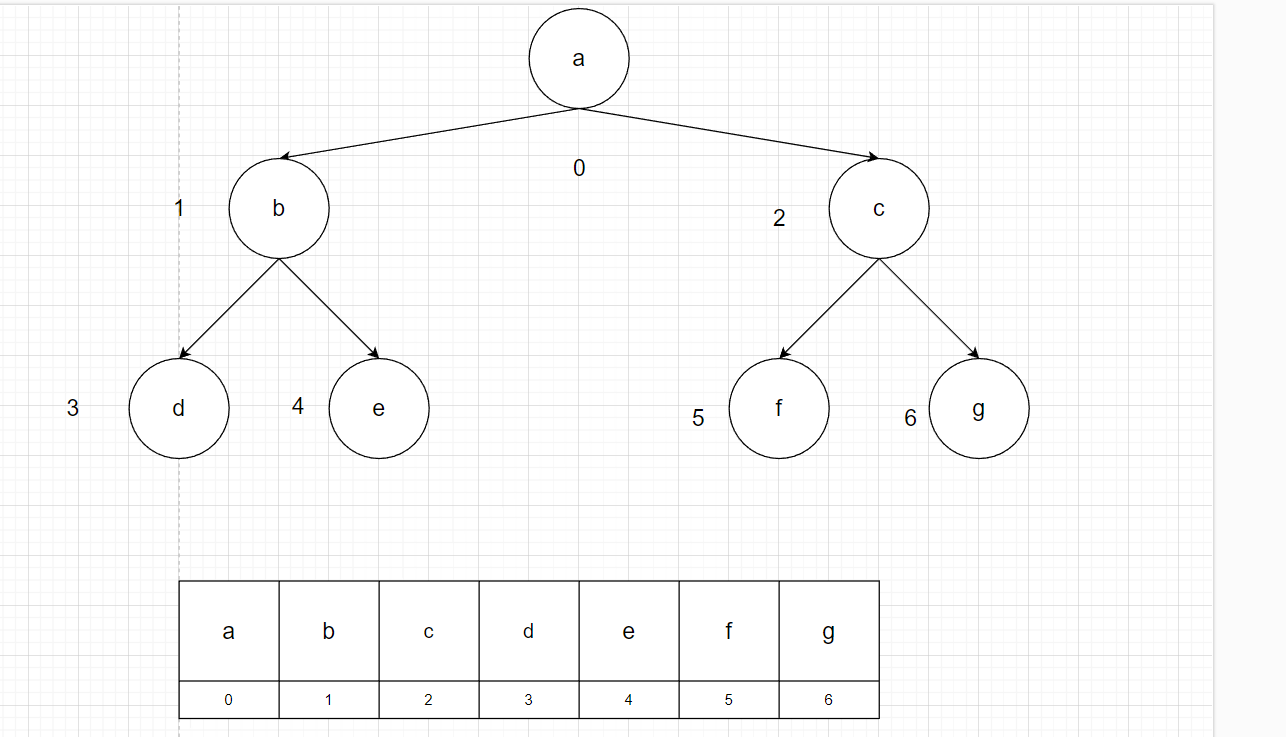
存储方式如上图,设父节点的下标为i,左孩子节点为2i+1,右孩子节点为2i+2
缺点:树每次添加节点,数组有可能需要扩容;树里面可能有些节点没有分支,就会存储空值到数组里面,浪费空间。
优点:使用数组可以通过指定下标获取节点。
我们一般不使用数组来存储树的节点。
链式存储
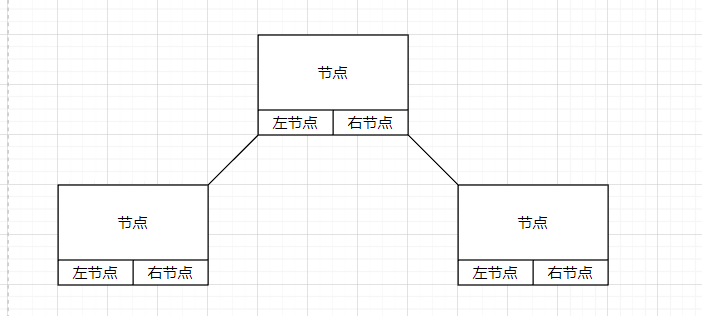
树的遍历方式
分为两个大类
- 层序遍历:先遍历完每一层的节点,然后再遍历下一层
- 深度遍历:从根节点一直遍历到叶子节点,然后再从叶子节点往回走
深度优先遍历
可以使用迭代法和递归法来实现
- 前序遍历:中左右
- 中序遍历:左中右
- 后续遍历:左右中
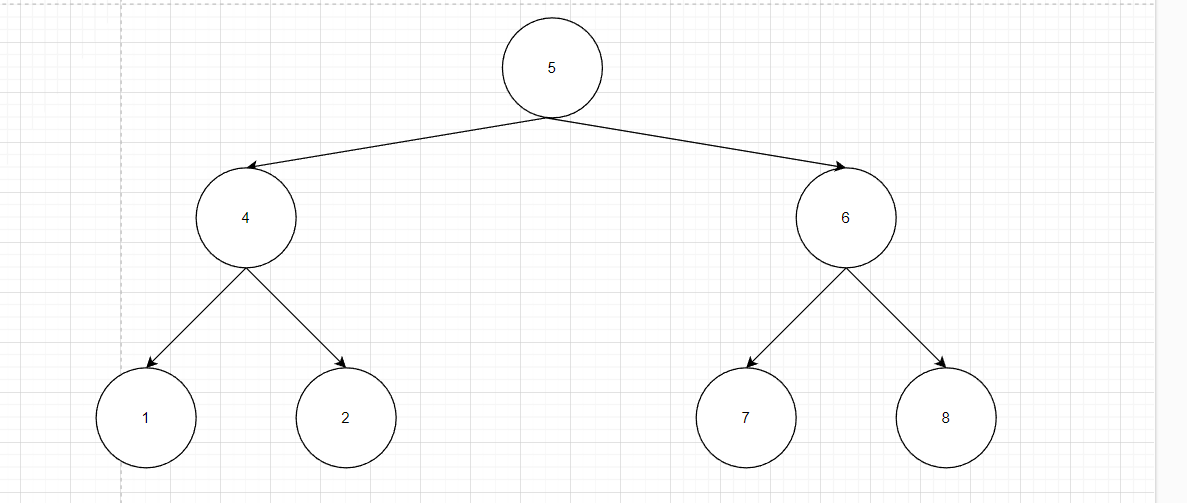
前序遍历: 5 4 1 2 6 7 8
中序遍历: 1 4 2 5 7 6 8
后续遍历: 1 2 4 7 8 6 5
广度优先遍历
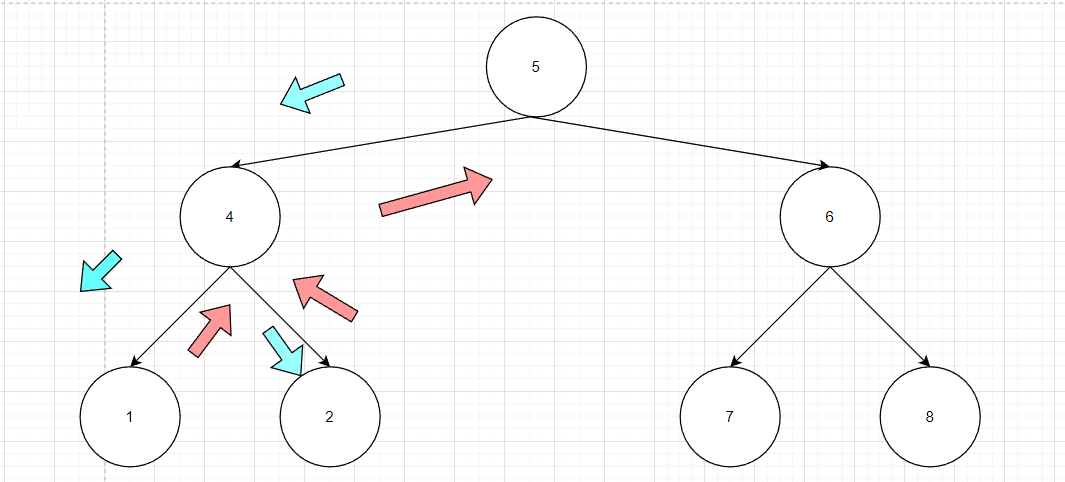
通过序列构造二叉树
我们可以通过序列来恢复原始的二叉树
(1) 前序:1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2) 中序:3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序:8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
前序和中序恢复二叉树
(1) 前序:1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2) 中序:3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
前序遍历:中左右
中序遍历:左中右
- 第一轮
我们可以定位到根节点,也就是1,通过中序遍历我们可以将左右子树分开
前序遍历
1 [2 3 4 5 6 8 7][ 9 10 11 12 13 15 14]
中序遍历
[3 4 8 6 7 5 2] 1 [10 9 11 15 13 14 12]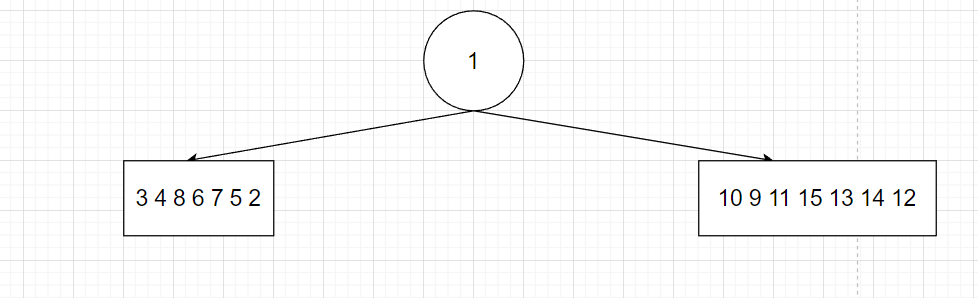
- 第二轮
通过前序遍历我们可以定位出
左树的根节点为2,并且没有右子树。
右树的根节点为9,左子树的节点为10
前序遍历
1 2 [3 4 5 6 7 8] 9 [10] [11 12 13 15 14]
中序遍历
[3 4 8 6 7 5] 2 1 [10] 9 [11 15 13 14 12]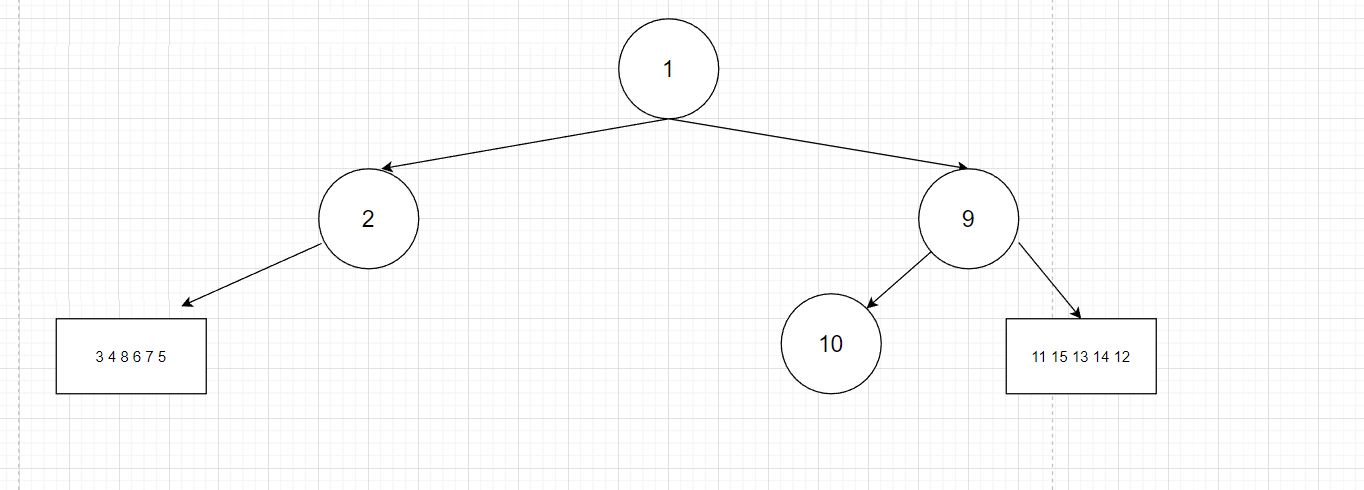
- 第三轮
前序遍历我们可以获取
左子树的根节点为3,里面没有左孩子
右子树的根节点为11,没有左孩子
前序遍历
3 [4 5 6 7 8] 11 [12 13 15 14]
中序遍历
3 [4 8 6 7 5] 11 [15 13 14 12]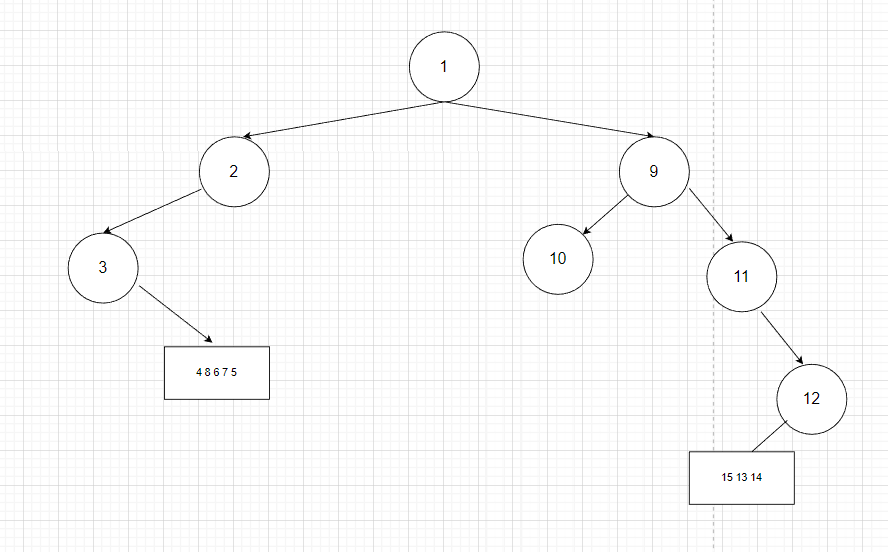
- 第四轮
左子树的根节点为4,没有左孩子
右子树的根节点为12,没有右子树
前序遍历
4 [5 6 7 8] 12 [13 15 14]
中序遍历
4 [8 6 7 5] [15 13 14 ] 12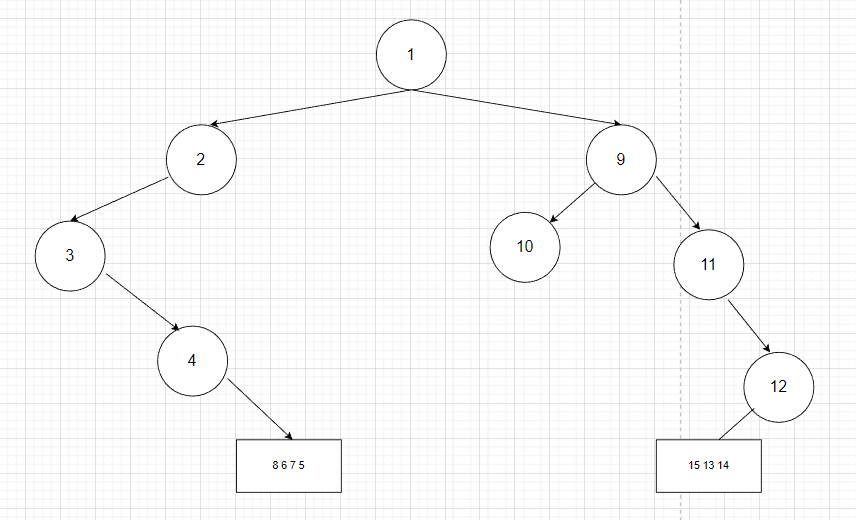
- 第五轮
左子树节点是5,没有右孩子
右子树节点是13,左孩子节点为15, 右孩子节点为14
前序遍历
5 [6 7 8] 13 [15 14]
中序遍历
[8 6 7 ] 5 [15] 13 [14 ]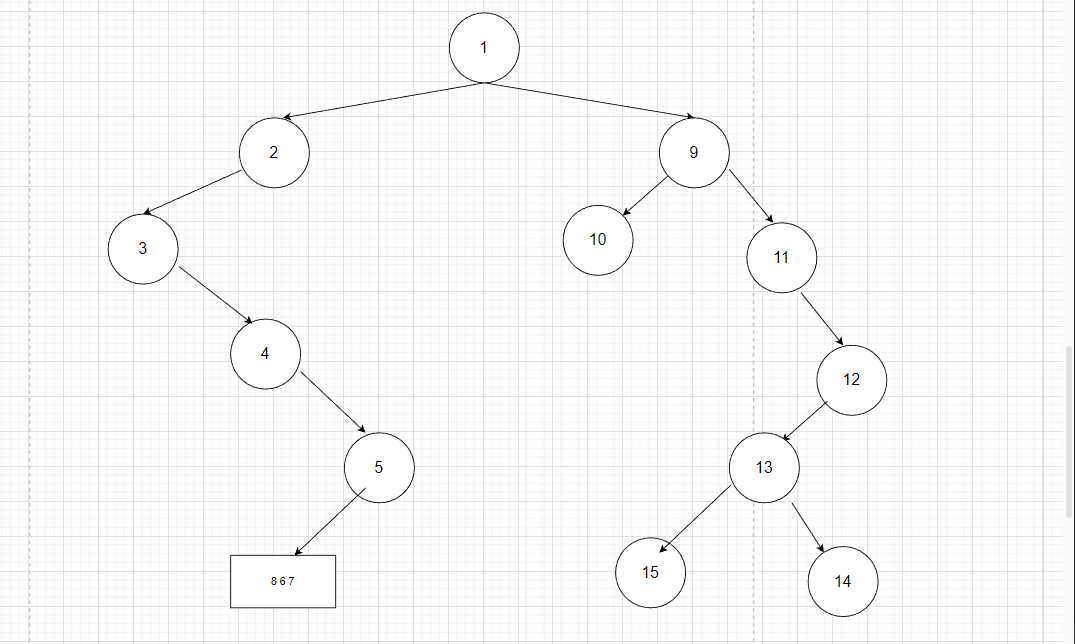
- 第六轮
6为根节点,左孩子为8,右孩子为7
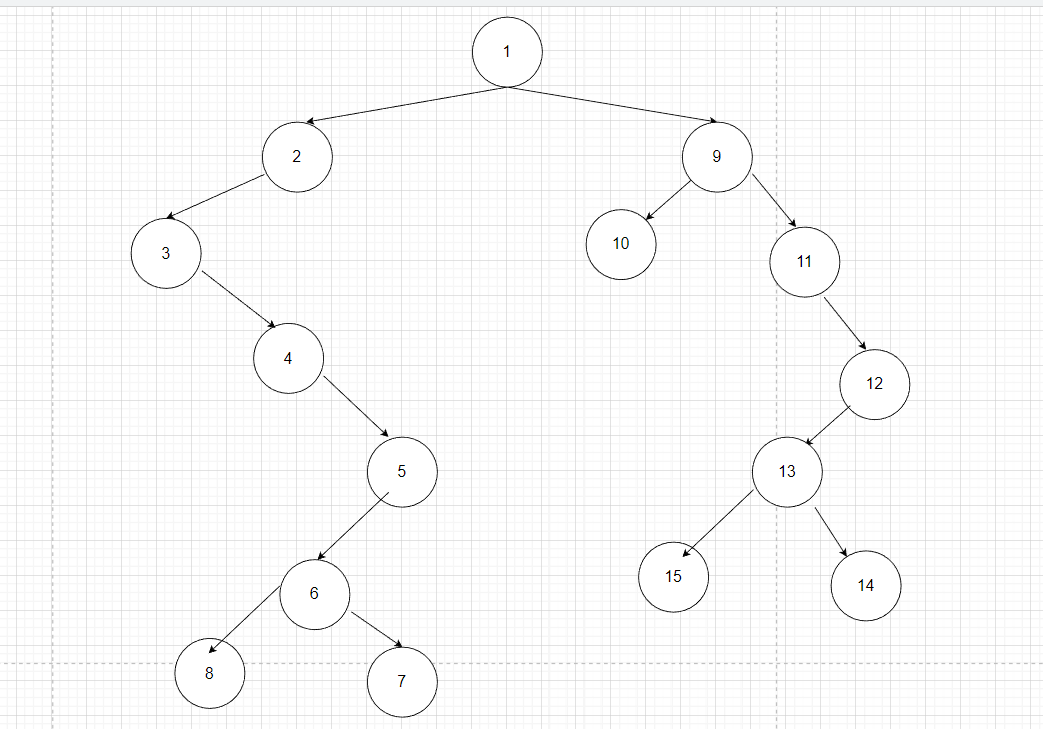
中序和后续恢复二叉树
基本类似上面的步骤
但是里面没有前序和后序的组合,因为我们无法获取到对应的左右子树的相关信息。
贡献者
flycodeu
版权所有
版权归属:flycodeu
